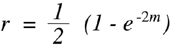
By the time the chemical nature of the gene was uncovered, genetics was already a mature science. In fact, Mendel's formulation of the basic principles of heredity was not even dependent on an understanding of the fact that genes existed within chromosomes. Rather, the existence of genes was inferred solely from the expression in offspring of visible traits at predicted frequencies based on the traits present in the parental and grandparental generations. Today, of course, the field of genetics encompasses a broad spectrum of inquiry from molecular studies on gene regulation to analyses of allele frequencies in natural populations, with many subfields in between. To distinguish the original version of genetics — that of Mendel and his followers — from the various related fields that developed later, several terms have been coined including "formal" genetics, "transmission" genetics, or "classical" genetics. Transmission genetics is the most informative term since it speaks directly to the feature that best characterizes the process by which Mendelian data are obtained — through an analysis of the transmission of genotypes and phenotypes from parents to offspring.
Mendel himself only formulated two of the three general features that underlie all studies in transmission genetics from sexually reproducing organisms. His formulations have been codified into two laws. The first law states, in modern terms, that each individual carries two copies of every gene and that only one of these two copies is transmitted to each child. At the other end of this equation, a child will receive one complete set of genes from each parent, leading to the restoration of a genotype that contains two copies of every gene. Individuals (and cells) that carry two copies of each gene are considered "diploid."
Mendel's first law comes into operation when diploid individuals produce "haploid" gametes — sperm or eggs — that each carry only a single complete set of genes. In animals, only a certain type of highly specialized cell — known as a "germ cell" — is capable of undergoing the transformation from the diploid to the haploid state through a process known as meiosis. At the cell division in which this transformation occurs, the two copies of each gene will separate or segregate from each other and move into different daughter (or brother) cells. This event provides the name for Mendel's first law: "the law of segregation." Segregation can only be observed from loci that are heterozygous with two distinguishable alleles. As a result of segregation, half of an individual's gametes will contain one of these alleles and half will contain the other. Thus, a child can receive either allele with equal probability. 43
While Mendel's first law is concerned with the transmission of individual genes in isolation from each other, his second law was formulated in an attempt to codify the manner in which different genes are transmitted relative to each other. In modern terms, Mendel's second law states that the segregation of alleles from any one locus will have no influence on the segregation of alleles from any other locus. In the language of probability, this means that each segregation event is independent of all others and this provides the name for Mendel's second law: "the law of independent assortment."
Independent assortment of alleles at two different loci — for example, A and B — can only be observed from an individual who is heterozygous at both with a genotype of the form A/a, B/b as illustrated in Figure 7.2. Each gamete produced by such an individual will carry only one allele from the A locus and only one allele from the B locus. Since the two alleles are acquired independently of each other, it is possible to calculate the probability of any particular allelic combination by simply multiplying together the probability of occurrence of each alone. For example, the probability that a gamete will receive the A allele is 0.5 (from the law of segregation) and the probability that this same gamete will receive the b allele is similarly 0.5. Thus, the probability that a gamete will have a combined A b genotype is 0.5 x 0.5 = 0.25. The same probabilities are obtained for all four possible allelic combinations (A B, a b, A b, a B). Since the number of gametes produced by an individual is very large, these probabilities translate directly into the frequencies at which each gamete type is actually present and, in turn, the frequency with which each will be transmitted to offspring (Figure 7.2).
As we all know today, Mendel's second law holds true only for genes that are not linked together on the same chromosome. 44 When genes A and B are linked, the numbers expected for each of the four allele sets becomes skewed from 25% (Figure 7.3). Two allele combinations will represent the linkage arrangements on the parental chromosomes (for example, A B and a b), and these combinations will each be transmitted at frequency of greater than 25%. The remaining two classes will represent recombinant arrangements that will be transmitted at a frequency below 25%. In the extreme case of absolute linkage, only the two parental classes will be transmitted, each at a frequency of 50%. At intermediate levels of linkage, transmission of the two parental classes together will be greater than 50% but less than 100%.
In 1905, when evidence for linkage was first encountered in the form of loci whose alleles did not assort independently, its significance was not appreciated (Bateson et al., 1905). The terms coupling and repulsion were coined to account for this unusual finding through some sort of underlying physical force. In a genetics book from 1911, Punnett imagined that alleles of different genes might "repel one another, refusing, as it were, to enter into the same zygote, or they may attract one another, and becoming linked, pass into the same gamete, as it were by preference" (Punnett, 1911). What this hypothesis failed to explain is why alleles found in repulsion to each other in one generation could become coupled to each other in the next generation. But even as Punnett's genetics text was published, an explanation was at hand. In 1912, Morgan and his colleagues proposed that coupling and repulsion were actually a consequence of co-localization of genes to the same chromosome: coupled alleles are those present on the same parental homolog, and alleles in repulsion are those present on alternative homologs (Morgan and Cattell, 1912 and Figure 7.3). Through the process of crossing over, alleles that are in repulsion in one generation (for example the A and b alleles in Figure 7.3) can be brought together on the same homolog — and thus become coupled — in the next generation. In 1913, Sturtevant used the rates at which crossing over occurred between different pairs of loci to develop the first linkage map with six genes on the Drosophila X chromosome (Sturtevant, 1913). Although the original rationale for the terms coupling and repulsion was eliminated with this new understanding, the terms themselves have been retained in the language of geneticists (especially human geneticists). Whether alleles at two linked loci are coupled or in repulsion is referred to as the phase of linkage.
The purpose of this chapter is to develop the concepts of transmission genetics as they are applied to contemporary studies of the mouse. This discussion is not meant to be comprehensive. Rather, it will focus on the specific protocols and problems that are most germane to investigators who seek to place genes onto the mouse linkage map and those who want to determine the genetic basis for various traits that are expressed differently by different animals or strains.
Genetic linkage is a direct consequence of the physical linkage of two or more loci within the same pair of DNA molecules that define a particular set of chromosome homologs within the diploid genome. Genetic linkage is demonstrated in mice through breeding experiments in which one or both parents are detectably heterozygous at each of the loci under investigation. In the simplest form of linkage analysis — referred to as a backcross — only one parent is heterozygous at each of two or more loci, and the other parent is homozygous at these same loci. As a result, segregation of alternative alleles occurs only in the gametes that derive from one parent, and the genotypes of the offspring provide a direct determination of the allelic constitution of these gametes. The backcross greatly simplifies the interpretation of genetic data because it allows one to jump directly from the genotypes of offspring to the frequencies with which different meiotic products are formed by the heterozygous parent.
For each locus under investigation in the backcross, one must choose appropriate heterozygous and homozygous genotypes so that the segregation of alleles from the heterozygous parents can be followed in each of the offspring. For loci that have not been cloned, the genotype of the offspring can only be determined through a phenotypic analysis. In this case, if the two alleles present in the heterozygous parent show a complete dominant/recessive relationship, then the other parent must be homozygous for the recessive allele. For example, the A allele at the agouti locus causes a mouse to have a banded "agouti" coat color, whereas the a allele determines a solid "non-agouti" coat color. Since the A allele is dominant to a, the homozygous parent must be a/ a. In an A/ a x a/ a backcross, the occurrence of agouti offspring would indicate the transmission of the A allele from the heterozygous parent, and the occurrence of non-agouti offspring would indicate the transmission of the a allele.
In the case just described, the wild-type allele (A) is dominant and the mutant allele (a) is recessive. Thus, the homozygous parent must carry the mutant allele (a/ a) and express a non-agouti coat color. In other cases, however, the situation is reversed with mutations that are dominant and wild-type alleles that are recessive. For example, the T mutation at the T locus causes a dominant shortening of the tail. Thus, if the T locus were to be included in a backcross, the heterozygous genotype would be T/+ and the homozygous genotype would be wild-type (+/+) to allow one to distinguish the transmission of the T allele (within short-tailed offspring) from the + allele (within normal-tailed offspring).
As discussed in Chapter 8, most loci are now typed directly by DNA-based techniques. As long as both DNA alleles at a particular locus can be distinguished from each other, 45 it does not matter which is chosen for inclusion in the overall genotype of the homozygous parent. The same holds true for all phenotypically defined loci at which pairs of alleles act in a codominant or incompletely dominant manner. In all these cases, the heterozygote (A1/A2 for example) can be distinguished from both homozygotes (A1/A1 and A2/A2).
In the example presented in Figure 7.3, an animal is heterozygous at both of two linked loci, which results in two complementary sets of coupled alleles — A B and a b. The genotype of this animal would be written as follows: AB/ab. 46 In the absence of crossing over between homologs during meiosis, one or the other coupled set — either A B or a b — will be transmitted to each gamete. However, if a crossover event does occur between the A and B loci, a non-parental combination of alleles will be transmitted to each gamete. In the example shown in Figure 7.3, the frequency of recombination between loci A and B can be calculated directly by determining the percentage of offspring formed from gametes that contain one of the two non-parental, or "recombinant," combinations of alleles. In this example, the recombination frequency is 10%.
To a first degree, crossing over occurs at random sites along all of the chromosomes in the genome. A direct consequence of this randomness is that the farther apart two linked loci are from each, the more likely it is that a crossover event will occur somewhere within the length of chromosome that lies between them. Thus, the frequency of recombination provides a relative estimate of genetic distance. Genetic distances are measured in centimorgans (cM) with one centimorgan defined as the distance between two loci that recombine with a frequency of 1%. Thus, as a further example, if two loci recombine with a frequency of 2.5%, this would represent an approximate genetic distance of 2.5 cM. In the mouse, correlations between genetic and physical distances have demonstrated that one centimorgan is, on average, equivalent to 2,000 kilobases. It is important to be aware, however, that the rate of equivalence can vary greatly due to numerous factors discussed in Section 7.2.3.
Although the frequency of recombination between two loci is roughly proportional to the length of DNA that separates them, when this length becomes too large, the frequency will approach 50%, which is indistinguishable from that expected with unlinked loci. The average size of a mouse chromosome is 75 cM. Thus, even when genes are located on the same chromosome, they are not necessarily linked to each other according to the formal definition of the term. However, a linkage group does include all genes that have been linked by association. Thus, if gene A is linked to gene B, and gene B is linked to gene C, the three genes together — A B C — form a linkage group even if the most distant members of the group do not exibit linkage to each other.
A priori, one might assume that all recombination events within the same meiotic cell should be independent of each other. A direct consequence of this assumption is that the linear relationship between recombination frequency and genetic distance — apparent in the single digit centimorgan range — should degenerate with increasing distances. The reason for this degeneration is that as the distance between two loci increases, so does the probability that multiple recombination events will occur between them. Unfortunately, if two, four, or any other even number of crossovers occur, the resulting gametes will still retain the parental combination of coupled alleles at the two loci under analysis as shown in Figure 7.4. Double (as well as quadruple) recombinants will not be detectably different from non-recombinants. As a consequence, the observed recombination frequency will be less than the actual recombination frequency.
Consider, for example, two loci that are separated by a real genetic distance of 20 cM. According to simple probability theory, the chance that two independent recombination events will occur in this interval is the product of the predicted frequencies with which each will occur alone which is 0.20 for a 20 cM distance. Thus, the probability of a double recombination event is 0.2 x 0.2 = 0.04. The failure to detect recombination in 4% of the gametes means that two loci separated by 20 cM will only show recombination at a frequency of 0.16. 47 A similar calculation indicates that at 30 cM, the observed frequency of recombinant products will be even further removed at 0.21. In 1919, Haldane simplified this type of calculation by developing a general equation that could provide values for recombination fractions at all map distances based on the formulation just described. This equation is known as the "Haldane mapping function" and it relates the expected fraction of offspring with detectable recombinant chromosomes (r) to the actual map distance in morgans (m) 48 that separates the two loci (Haldane, 1919):
After working through this hypothetical adjustment to recombination rates, it is now time to state that multiple events of recombination on the same chromosome are not independent of each other. In particular, a recombination event at one position on a chromosome will act to interfere with the initiation of other recombination events in its vicinity. This phenomenon is known, appropriately, as "interference." Interference was first observed within the context of significantly lower numbers of double crossovers than expected in the data obtained from some of the earliest linkage studies conducted on Drosophila (Muller, 1916). Since that time, interference has been demonstrated in every higher eukaryotic organism for which sufficient genetic data have been generated.
Significant interference has been found to extend over very long distances in mammals. The most extensive quantitative analysis of interference has been conducted on human chromosome 9 markers that were typed in the products of 17,316 meiotic events (Kwiatkowski et al., 1993). Within 10 cM intervals, only two double-crossover events were found; this observed frequency of 0.0001 is 100-fold lower than expected in the absence of interference. Within 20 cM intervals, there were 10 double-crossover events (including the two above); this observed frequency of 0.0005 is still 80-fold lower than predicted without interference. As map distances increase beyond 20 cM, the strength of interference declines, but even at distances of up to 50 cM, its effects can still be observed (Povey et al., 1992). 49
If one assumes that human chromosome 9 is not unique in its recombinational properties, the implication of this analysis is that for experiments in which fewer than 1,000 human meiotic events are typed, multiple crossovers within 10 cM intervals will be extremely unlikely, and within 25 cM intervals, they will still be quite rare. Data evaluating double crossovers in the mouse are not as extensive, but they suggest a similar degree of interference (King et al., 1989). Thus, for all practical purposes, it is appropriate to convert recombination fractions of 0.25, or less, directly into centimorgan distances through a simple multiplication by 100.
When it is necessary to work with recombination fractions that are larger than 0.25, it is helpful to use a mapping function that incorporates interference into an estimate of map distance. Since the effects of interference can only be determined empirically, one cannot derive such a mapping function from first principles.
Instead, equations have been developed that fit the results observed in various species (Crow, 1990). The best-known and most widely-used mapping function is an early one developed by Kosambi (1944):
By solving Equation 7.2 for the observed recombination fraction, r, one obtains the "Kosambi estimate" of the map distance, mK, which is converted into centimorgans through multiplication by 100. Later, Carter and Falconer (1951) developed a mapping function that assumes even greater levels of interference based on the results obtained with linkage studies in the mouse: 50
Although it is clear that the Carter-Falconer mapping function is the most accurate for mouse data, the Kosambi equation was more easily solvable in the days before cheap, sophisticated hand-held calculators were available. Although the Carter-Falconer function is readily solvable today, it is not as well-known and not as widely used.
Interference works to the benefit of geneticists performing linkage studies for two reasons. First, the approximate linearity between recombination frequency and genetic distance is extended out much further than anticipated from strictly independent events. 51 Second, the very low probability of multiple recombination events can serve as a means for distinguishing the correct gene order in a three-locus cross, since any order that requires double recombinants among markers within a 20 cM interval is suspect. When all possible gene orders require a double or triple crossover event, it behooves the investigator to go back and re-analyze the sample or samples in which the event supposedly occurred. Finally, if the genotypings are shown to be correct, one must consider the possibility that an isolated gene conversion event has occurred at the single locus that differs from those flanking it.
Although genetic interference will restrict the randomness with which crossover events are distributed relative to each other within individual gametes, it will not affect the random distribution of crossover sites observed in large numbers of independent meiotic products. Thus, a priori, one would still expect the resolution of a linkage map to increase linearly with the number of offspring typed in a genetic cross. Assuming random sites of recombination, the average distance, in centimorgans, between crossover events observed among the offspring from a cross can be calculated according to the simple formula (100/N) where N is the number of meiotic events that are typed. For example, in an analysis of 200 meiotic events (200 backcross offspring or 100 intercross offspring), one will observe, on average, one recombination event every 0.5 cM. With 1,000 meiotic events, the average distance will be only 0.1 cM which is equivalent to approximately 200 kb of DNA. Going further according to this formula, with 10,000 offspring, one would obtain a genetic resolution that approached 20 kb. This would be sufficient to separate and map the majority of average-size genes in the genome relative to each other.
Once again, however, the results obtained in actual experiments do not match the theoretical predictions. In fact, the distribution of recombination sites can deviate significantly from randomness at several different levels. First, in general, the telomeric portions of all chromosomes are much more recombinogenic than are those regions closer to the centromere in both mice (de Boer and Groen, 1974) and humans (Laurie and Hulten, 1985). This effect is most pronounced in males and it leads to an effect like a rubber band when one tries to orient male and female linkage maps relative to each other (Donis-Keller et al., 1987). Second, different sites along the entire chromosome are more or less prone to undergo recombination. Third, even within the same genomic region, rates of recombination can vary greatly depending on the particular strains of mice used to produce the hybrid used for analysis (Seldin et al., 1989; Reeves et al., 1991; Watson et al., 1992). Finally, the sex of the hybrid can also have a dramatic effect on rates of recombination (Reeves et al., 1991).
Gender-specific differences in recombination rates are well known. In general, it can be stated that recombination occurs less frequently during male meiosis than during females meiosis. An extreme example of this general rule is seen in Drosophila melanogaster where recombination is eliminated completely in the male. In the mouse, the situation is not as extreme with males showing a rate of recombination that is, on average, 50-85% of that observed in females (Davisson et al., 1989). However, the ratio of male to female rates of recombination can vary greatly among different regions of the mouse genome. In a few regions, the recombination rates are indistinguishable between sexes, and in even fewer regions yet, the male rates of recombination exceed female rates. Nevertheless, the general rule of higher recombination rates in females can be used to maximize data generation by choosing gender appropriately for a heterozygous F1 animal in a backcross. For example, to maximize chances of finding initial evidence for linkage, one could choose males as the F1 animals, but to maximize the resolution of a genetic map in a defined region, it would be better to use females. These considerations are discussed further in Section 9.4.
The most serious blow to the unlimited power of linkage analysis has come from the results of crosses in which many thousands of offspring have been typed for recombination within small well-defined genomic regions. When the recombinant chromosomes generated in these crosses were examined at the DNA level, it was found that the distribution of crossover sites was far from random (Steinmetz et al., 1987). Instead, they tended to cluster in very small "recombinational hotspots" of a few kilobases or less in size (Zimmerer and Passmore, 1991; Bryda et al., 1992) The accumulated data suggest that these small hotspots may be distributed at average distances of several hundred kilobases apart from each other with 90% or more of all crossover events restricted to these sites.
The finding of recombinational hotspots in mice is surprising because it was not predicted from very high resolution mapping studies performed previously in Drosophila which showed an excellent correspondence between linkage and physical distances down to the kilobase level of analysis (Kidd et al., 1983). Thus, this genetic phenomenon — like genomic imprinting (Section 5.5) — might be unique to mammals. Unlike imprinting, however, the locations of particular recombinational hotspots do not appear to be conserved among different subspecies or even among different strains of laboratory mice.
Figure 7.5 illustrates the consequences of hotspot-preferential crossing over on the relationship between linkage and physical maps. In this example, 2,000 offspring from a backcross were analyzed for recombination events between the fictitious A and F loci. These loci are separated by a physical distance of 1,500 kb and, in our example, 17 crossover events (indicated by short vertical lines on the linkage map) were observed among the 2,000 offspring. A recombination frequency of 17/2,000 translates into a linkage distance of 0.85 cM. This linkage distance is very close to the 0.75 cM predicted from the empirically determined equivalence of 2,000 kb to 1 cM. However, when one looks further at loci between A and F, the situation changes dramatically. The B and C loci are only 20 kb apart from each on the physical map but are 0.4 cM apart from each other on the linkage map because a hotspot occurs in the region between them. With random sites of crossing over, the linkage value of 0.4 cM would have predicted a physical distance of 800 kb. The reciprocal situation occurs for the loci D and E which are separated by a physical distance of 400 kb but which show no recombination in 2000 offspring. In this case, random crossing over would have predicted a physical distance of less than 100 kb.
The existence and consequences of recombinational hotspots can be viewed in analogy to the quantized nature of matter. For experiments conducted at low levels of resolution — for example, in measurements of grams or centimorgans — the distribution of both matter and crossover sites will appear continuous. At very high levels of resolution, however, the discontinuous nature of both will become apparent. In practical terms, the negative consequences of hotspots on the resolution of a mouse linkage map will only begin to show up as one goes below the 0.2 cM level of analysis.
With the limited number of very large sample linkage studies performed to date, it is not possible to estimate the portion of the mouse genome that is dominated by hotspot-directed recombination. Furthermore, it is still possible that some genomic regions will allow unrestricted recombination as in Drosophila. Nevertheless, the available data suggest that for much of the genome, there will be an upper limit to the resolution that can be achieved in linkage studies based on a single cross. This limit will be reached at a point when the density of crossover sites passes the density of hotspots in the region under analysis. From the data currently available, it appears likely that this point will usually be crossed before one reaches 500 meiotic events corresponding to 0.2 cM or 400 kb. One strategy that can be used to overcome this limitation is to combine information obtained from several crosses with different unrelated inbred partners, each of which is likely be associated with different hotspot locations. This approach is discussed more fully in Section 9.4.
As mentioned previously, the telomeric portions of chromosomes show higher rates of recombination per DNA length than more centrally located chromosomal regions. However, there is still great variation in recombination rates even among different non-telomeric regions. Some 1 mb regions produce recombinants at a rate equivalent to 2 cM or greater, whereas other regions of equivalent size only recombine with a rate equivalent to 0.5 cM or less in animals of the same gender. This variation could be due to differences in the number and density of recombination hotspots. In addition, the "strength" of individual hotspots, in terms of recombinogenicity, may differ from one site to another. Such differences could be specified by the DNA sequences at individual hotspots or by the structure of the chromatin that encompass multiple hotspots in a larger interval. A final variable may be generalized differences in the rates at which recombination can occur in regions between hotspots. Many more empirical studies will be required to sort through these various explanations.
Although its significance was not immediately recognized, the first demonstration of linkage in the mouse was published in 1915 by the great twentieth century geneticist J.B.S. Haldane (1915). What Haldane found was evidence for coupling between mutations at the albino (c) and pink-eyed dilution (p) loci, which we now know to lie 15 cM apart on Chr 7. Since that time, the linkage map of the mouse has expanded steadily at a near-exponential pace. During the first 65 years of work on the mouse map, this expansion took place one locus at a time. First, each new mutation had to be bred into a strain with other phenotypic markers. Then further breeding was pursued to determine whether the new mutation showed linkage to any of these other markers. This process had to be repeated with different groups of phenotypic markers until linkage to one other previously mapped marker was established. At this point, further breeding studies could be conducted with additional phenotypic markers from the same linkage group to establish a more refined map position.
In the first compendium of mouse genetic data published in the Biology of the Laboratory Mouse in 1941 (Snell, 1941), a total of 24 independent loci were listed, of which 15 could be placed into seven linkage groups containing either two or three loci each; the remaining nine loci were found not to be linked to each other or to any of the seven confirmed linkage groups. By the time the second edition of the Biology of the Laboratory Mouse was published in 1966, the number of mapped loci had grown to 250, and the number of linkage groups had climbed to 19, although in four cases, these included only two or three loci (Green, 1966).
With the 1989 publication of the second edition of the Genetic Variants and Strains of the Laboratory Mouse (Lyon and Searle, 1989), 965 loci had been mapped on all 20 recombining chromosomes. However, even at the time that this map was actually prepared for publication (circa late 1987), it was still the case that the vast majority of mapped loci were defined by mutations that had been painstakingly incorporated into the whole genome map through extensive breeding studies.
The first important conceptual breakthrough aimed at reducing the time, effort, and mice required to map single loci came with the conceptualization and establishment of recombinant inbred (abbreviated RI) strains by Donald Bailey and Benjamin Taylor at the Jackson Laboratory (Bailey, 1971; Taylor, 1978; Bailey, 1981). As discussed in detail in Section 9.2, a set of RI strains provides a collection of samples in which recombination events between homologs from two different inbred strains are preserved within the context of new inbred strains. The power of the RI approach is that loci can be mapped relative to each other within the same "cross" even though the analyses themselves may be performed many years apart. Since the RI strains are essentially preformed and immortal, typing a newly defined locus requires only as much time as the typing assay itself.
Although the RI mapping approach was extremely powerful in theory, during the first two decades after its appearance, its use was rather limited because of two major problems. First, analysis was only possible with loci present as alternative alleles in the two inbred parental strains used to form each RI set. This ruled out nearly all of the many loci that were defined by gross phenotypic effects. Only a handful of such loci — primarily those that affect coat color — were polymorphic among different inbred strains. In fact, in the prerecombinant DNA era, the only other loci that were amenable to RI analysis were those that encoded: (1) polymorphic enzymes (called allozymes or isozymes) that were observed as differentially migrating bands on starch gels processed for the specific enzyme activity under analysis (Womack, 1979); (2) immunological polymorphisms detected at minor histocompatibility loci (Graff, 1978); and (3) other polymorphic cell surface antigens (called alloantigens or isoantigens) that could be distinguished with specially developed "allo-antisera" (Boyse et al., 1968). In retrospect, it is now clear that RI strains were developed ahead of their time; their power and utility in mouse genetics is only now — in the 1990s — being fully unleashed.
Two events that occurred during the 1980s allowed the initial development of a whole genome mouse map that was entirely based on DNA marker loci. The first event was the globalization of the technology for obtaining DNA clones from the mouse genome and all other organisms. Although the techniques of DNA cloning had been developed during the 1970s, stringent regulations in the U.S. and other countries had prevented their widespread application to mammalian species like the mouse (Watson and Tooze, 1981). These regulations were greatly reduced in scope during the early years of the 1980s so that investigators at typical biological research facilities could begin to clone and characterize genes from mice. The globalization of the cloning technology was greatly hastened in 1982 by the publication of the first highly detailed cloning manual from Cold Spring Harbor Laboratory, officially entitled Molecular Cloning: A Laboratory Manual, but known unofficially as "The Bible" (Maniatis et al., 1982). 52
Although DNA clones were being recovered at a rapid rate during the 1980s, from loci across the mouse genome, their general utilization in linkage mapping was not straightforward. The only feasible technique available at the time for mapping cloned loci was the typing of restriction fragment length polymorphisms (RFLPs). Unfortunately, as discussed earlier in this book (Sections 2.3 and 3.2), the common ancestry of the traditional inbred strains made it difficult, if not impossible, to identify RFLPs between them at most cloned loci.
The logjam in mapping was broken not through the development of a new molecular technique, but rather, through the development of a new genetic approach. This was the second significant event in terms of mouse mapping during the 1980s — the introduction of the interspecific backcross. François Bonhomme and his French colleagues had discovered that two very distinct mouse species — M. musculus and M. spretus — could be bred together in the laboratory to form fertile F1 female hybrids (Bonhomme et al., 1978). With the three million years that separate these two Mus species (Section 2.3), basepair substitutions have accumulated to the point where RFLPs can be rapidly identified for nearly every DNA probe that is tested. Thus, by backcrossing an interspecific super-heterozygous F1 female to one of its parental strains, it becomes possible to follow the segregation of the great majority of loci that are identified by DNA clones through the use of RFLP analysis.
Although the "spretus backcross" could not be immortalized in the same manner as a set of RI strains, each of the backcross offspring could be converted into a quantity of DNA that was sufficient for RFLP analyses with hundreds of DNA probes. In essence, it became possible to move from a classical three-locus backcross to a several hundred locus backcross. Furthermore, the number of loci could continue to grow as new DNA probes were used to screen the members of the established "mapping panel" (until DNA samples were used up). The spretus backcross revolutionized the study of mouse genetics because it provided the first complete linkage map of the mouse genome based on DNA markers and because it provided mapping panels that could be used to rapidly map essentially any new locus that was defined at the DNA level.
The most recent major advance in genetic analysis has come not from the development of new types of crosses but from the discovery and utilization of PCR-based DNA markers that are extremely polymorphic and can be rapidly typed in large numbers of animals with minimal amounts of sample material. These powerful new markers — especially microsatellites — have greatly diminished the essential need for the spretus backcross and they have breathed new life into the usefulness of the venerable RI strains. Most importantly, it is now possible for individual investigators with limited resources to carry out independent, sophisticated mapping analyses of mutant genes or complex disease traits. As Philip Avner of the Institut Pasteur in Paris states: "If the 1980s were the decade of Mus spretus — whose use in conjunction with restriction fragment length polymorphisms revolutionized mouse linkage analysis, and made the mouse a formidably efficient system for genome mapping — the early 1990s look set to be the years of the microsatellite" (Avner, 1991). Microsatellites and other PCR-typable polymorphic loci are discussed at length in Section 8.3.